C6N: Topological lattice models at finite temperature
Michael Fleischhauer, Michael Köhl & Herwig Ott
Topology is an important paradigm for classifying phases of matter. It is well understood for ground states of Hamiltonians of non-interacting fermions, its generalization to finite-temperature- and non-equilibrium steady states is however still missing. In this joint theory-experiment project we will make fundamental steps in this direction. To this end, we study one-dimensional topological lattice models with interactions using two different experimental platforms: (i) Rydberg excitations with hard-core boson character in an array of optical tweezers, and (ii) ultra-cold spinful fermions in optical lattices subject to Hubbard interactions and in the presence of sharp edge potentials. We will perform the first measurement of the topological invariant for mixed states based on the ensemble geometric phase (EGP) and will investigate the fermionic Su-Shrieffer Heeger (SSH) and Rice Mele (RM) models with Hubbard interactions. Complementing the theory project C1 where a Z-type topological invariant for mixed-states of Chern-class systems is investigated, we will develop a theory for time-reversal invariant models with spin degrees of freedom and Z2-type invariants.
Finite-temperature topological invariant in Rydberg lattice systems
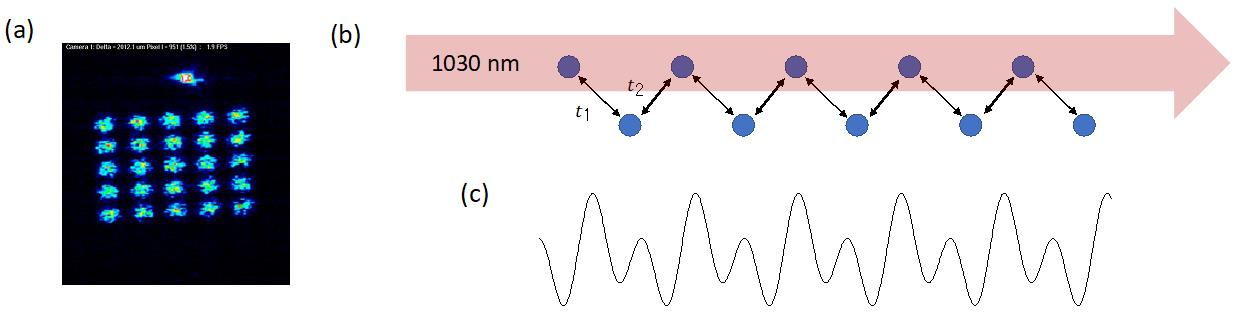
Fig.1: Optical tweezer setup and sketch of the realization of the SSH and RM model. (a) Two-dimensional array of optical dipole traps created by a spatial light modulator. (b) The SSH model implemented by chosing a zig-zag arrangement of the atoms. In order to realize the RM model, we will shine an additional off-resonant laser beam onto one chain of atoms, thus shifting their energy. (c) Effective potential in the presence of the dressing beam.
1D topological lattice models for interacting fermions
Here, we will extend our work to 1D topological lattice models with interactions. To this end, we study ultra-cold fermions with local Hubbard interaction between two spin components. Experimental indicators of non-trivial topology are edge states and quantized topological transport. Using developed techniques to create sharp potential steps, we will first investigate edge states and transport in the fermionic SSH and RM models with small or vanishing interactions. In a second step, we will consider strong interactions and low temperatures where gapped states with fractional filling and associated fractional topological charges emerge. Finally, we will modify the system to the time-reversal invariant version of the RM model, the Fu-Kane model.
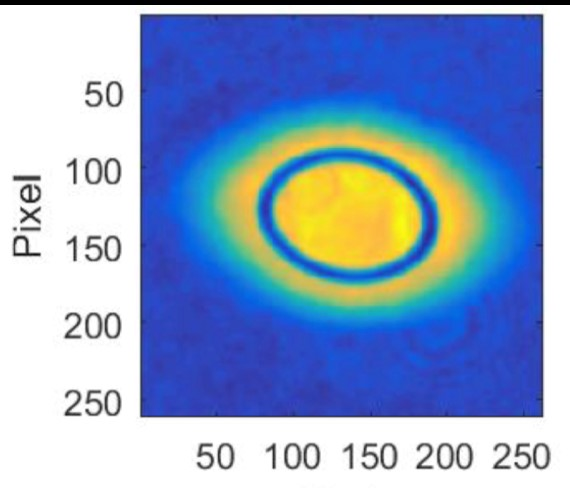
Fig.2: Image of atomic density distribution (1 pixel = 1 lattice site) with sharp boundaries. In the center there is a Hubbard system with homogeneous density, separated by a sharp potential barrier from the inhomogeneous remaining part of the cloud.
Finite-temperature topological invariant and time-reversal symmetry
The time-reversal (TR) invariant Fu-Kane model of spin-balanced fermions investigated experimentally in project part 2 leads to a quantized topological spin transport in opposite directions provided the fermions can be sufficiently cooled. It is thus natural to ask what topological features survive at finite temperatures in TR invariant systems, where the topological phase is characterized by a Z2 invariant instead of a Chern number? While the King-Smith Vanderbild relation between the Chern number and the many-body polarization allowed to introduce a topological invariant for finite-temperature states in systems with broken TR symmetry, the EGP, the generalization of the Z2 invariant to density matrices is unknown. In this theory project, we will develop such an invariant and investigate its properties.