Time-periodic driving of quantum systems has become an exciting tool to explore new states of matter and has been utilized to engineer effective fields and dynamically induced interactions in ultra-cold gas experiments.

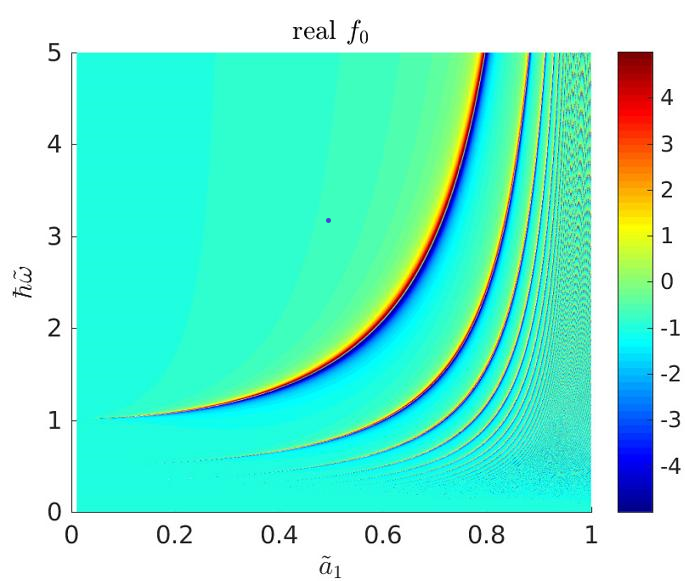
Theoretically, the corresponding steady states are described by an effective high-frequency expansion based on Floquet theory, which give a promising route for further exploration. At the same time, the full Floquet solution of the time-dependent Schodinger equation as a function of arbitrary frequency harbors potentially dramatic effects such as quantum resonance catastrophes, which cannot be predicted from the high frequency limit. It is therefore important to consider intermediate frequencies and moreover take decoherence and heating into account to take Floquet physics to the next level of quantum engineering, which is the motivation of this project.

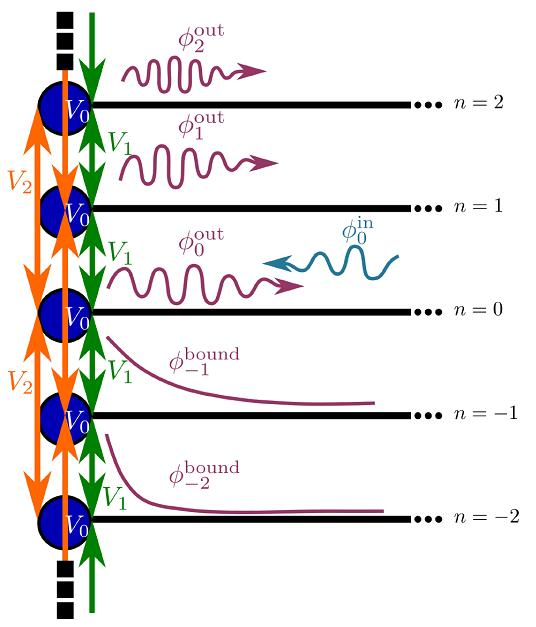
Going beyond the usual high-frequency approximation, we will analyze the full solution for selected many-body systems analytically and using our own newly developed Floquet-DMRG in the search of quantum resonance effects. In close collaboration with experiment we will furthermore consider few-body and non-interacting systems in order to address issues of stability, heating, and accessibility of the steady states, for which satisfactory theoretical predictions are still missing. In the framework of the SFB/TR issues of the topological character of the Floquet solutions, transport, induced resonances in 2-particle scattering and decohercence/heating effects will be addressed.