Topology is an important paradigm for classifying phases of matter. It is well understood for ground states of Hamiltonians of non-interacting fermions, its generalization to finite-temperature- and non-equilibrium steady states is however still missing. In the first funding period a topological invariant for Gaussian, i.e. non-interacting, mixed states applicable to Chern-class system was introduced and studied. In the second funding period we plan to extend this to interacting systems with fractional topological phases in one and two spatial dimensions.

Temperature induced topological phase transitions in interacting systems

Interaction -induced topological phases are an intensively studied field of research. By now there is a good understanding of symmetry-protected topology in one-dimensional interacting systems, yet the field is still far from a comprehensive understanding. Considering topological systems for which the ground-state physics is reasonably well understood, we will extend the work to finite-temperature and non-equilibrium steady states. In particular we will analyze if - in contrast to free systems - there is a temperature-induced topological phase transition and study the character of this transition.

Reservoir-induced and reservoir-stabilized fractional topological phases

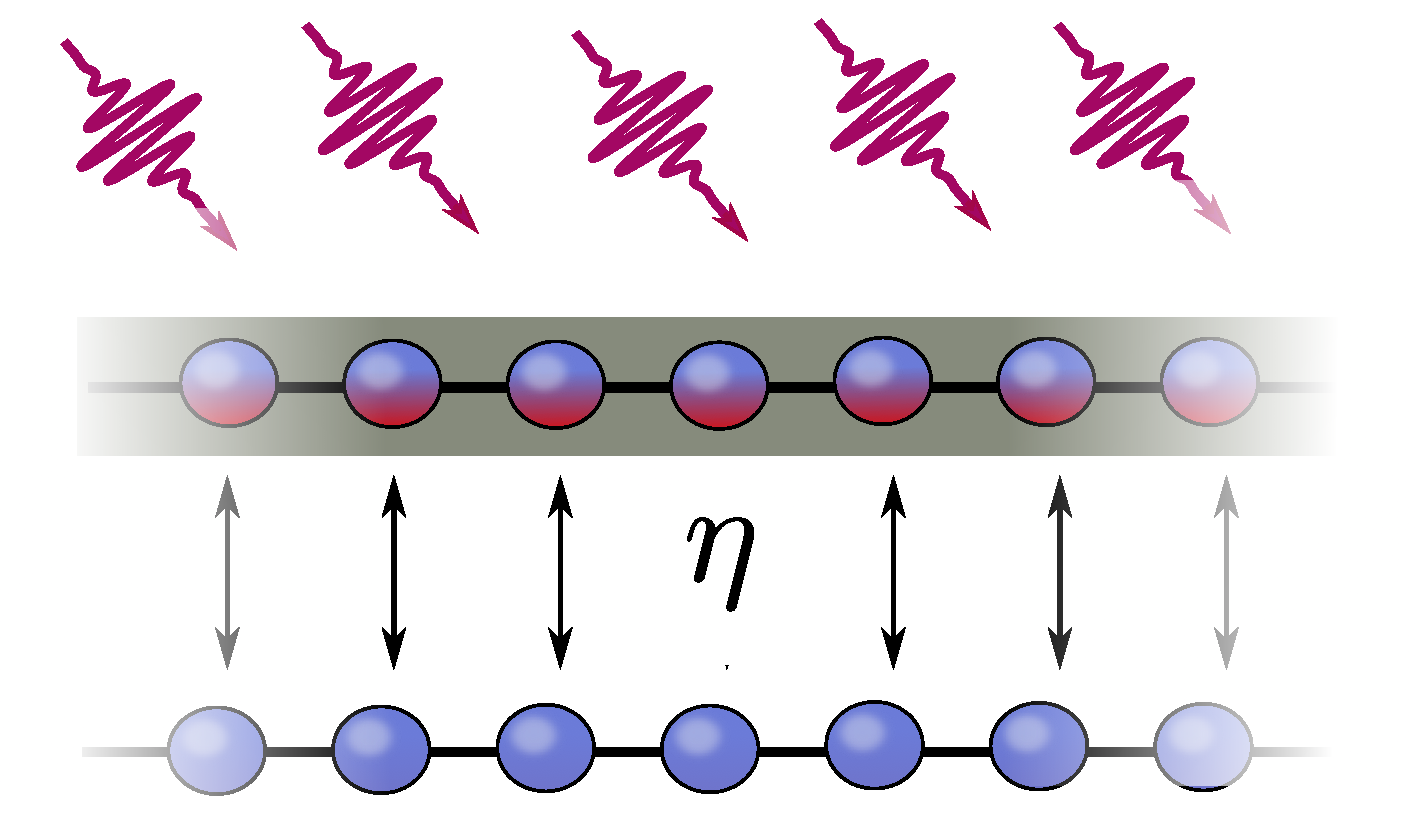
In the first funding period we have constructed topologically non-trivial models, such as an open-system analogue of the Rice-Mele model, where all topological features are induced solely by the action of Markovian reservoirs. The considered systems where however Gaussian and thus had integer topological charges. We will extend this to reservoirs that are nonlinear, as can be realized e.g. using Rydberg blockade in cold lattice gases (see B2, C6), allowing for degenerate steady states, fractional topological charges and fractional dissipative charge pumps.

Non-equilibrium topological equivalence classes of Gaussian systems of fermions

Our current understanding of topological insulators and superconductors is based on fundamental, non-spatial symmetries of the underlying Hamiltonians. Non interacting particles are fully described by hermitian matrices whose internal symmetries are time-reversal, (T), particle-hole or charge-conjugation (C), and chiral or sublattice symmetry (S = T C), which leads to the 10 Altland-Zirnbauer (AZ) symmetry classes. In recent years there is a growing interest to extend the AZ classification to open systems, approximated by non-hermitian Hamiltonians. The latter would result in 38 instead of 10 equivalence classes. The description of open systems in terms of non-hermitian matrices is however incomplete and additional constraints apply which reduces the number of possible classes. We will investigate non-equilibrium equivalence classes of open fermionic systems, concentrating on Gaussian, i.e. non-interacting, systems, as they are amenable to semi-analytic and numerical methods. This work will be done in collaboration with S. Diehl and A. Altland (Univ. Köln).

Physical consequences of finite-temperature and non-equilibrium topological invariants

The importance of topological invariants in unitary systems stems from the fact that they are responsible for a number of very intriguing physical effects. Here we will explore physical consequences of a quantized topological invariant of finite temperature or non-equilibrium steady states.