In topological systems out of equilibrium, stabilization of quantum transport in the presence of dissipation and/or many-body interactions is one of the most important issues. This project investigates, theoretically and experimentally, the quantization and stabilization of transport in one-dimensional topological lattice systems (dissipative and interacting Rice-Mele models) under nonadabatic periodic driving.

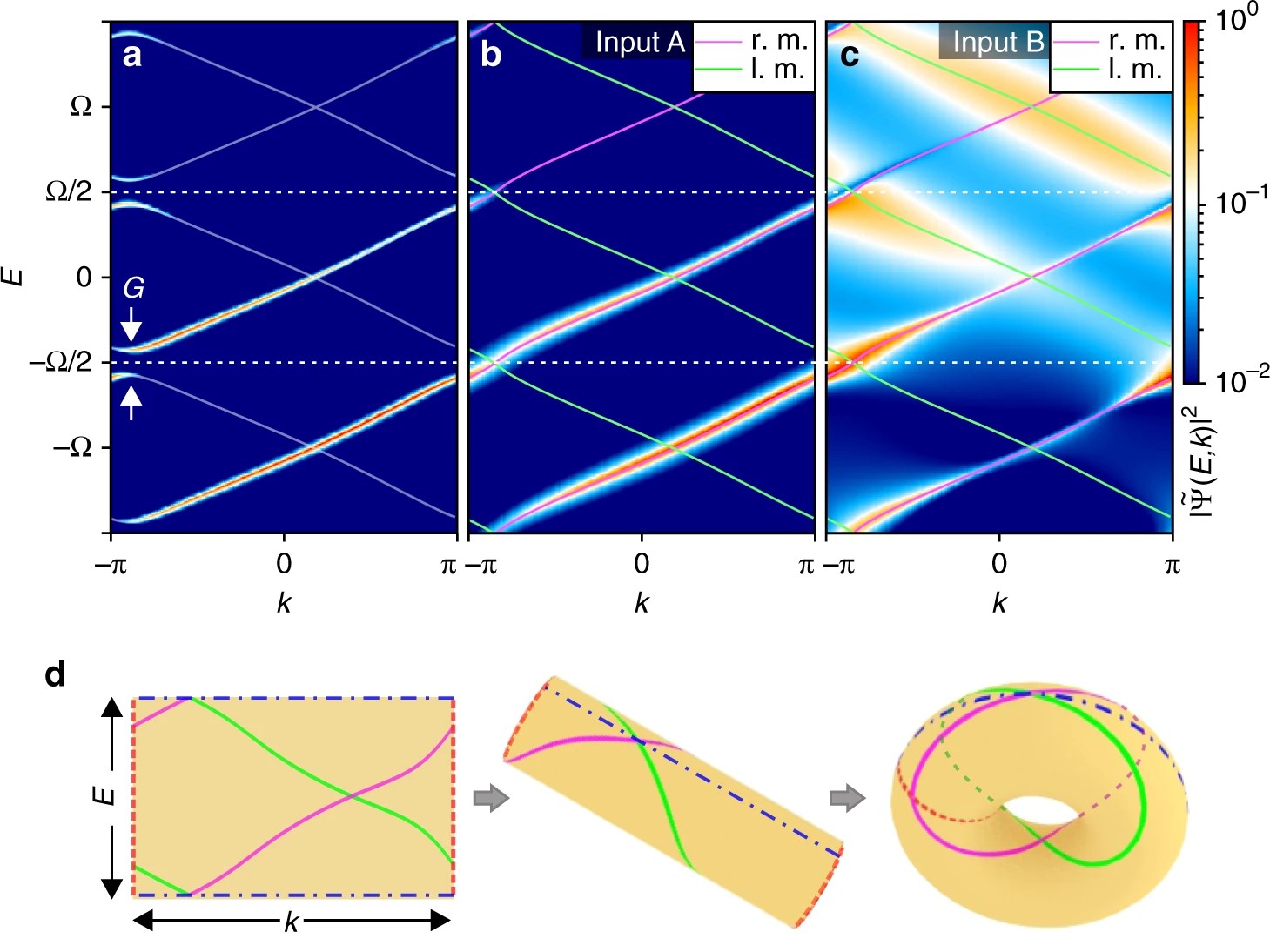
In the previous funding period, we have developed the Keldysh-Floquet Green’s function formalism for interacting, driven topological systems and computed interaction-induced quasiparticle relaxation rates. On part of the experiment, we have employed evanescently coupled plasmonic waveguide arrays (PWA) to demonstrate the existence of topological edge states as well as the scattering from a time-periodically driven impurity in Su-Schrieffer-Heeger topological PWAs. Jointly, we have discovered that a time-periodic modulation of the dissipation can restore quantized Thouless pumping in a nonadiabatically driven Rice-Mele system (see figure below). A crucial aspect in this context is the fact that PWAs are an exact representation of a dynamical quantum Hamiltonian, including the Berry phase arising in topological systems, since the electric-field envelope obeys a complex Schrödinger e quation, with the coordinate along the waveguide representing time.

In this funding period, we plan to investigate, in close collaboration of theory and experiment, the general conditions for dissipation-induced, fast (nonadiabatic) Thouless pumping. Experimentally, dissipative Rice-Mele models will be realized by tailoring the absorption properties of the PWAs. The knowledge gained will be applied theoretically to non-adiabatic Rice-Mele systems with dissipative, time-periodically modulated two-body interactions, realizable in ultracold gas systems. We will design Floquet topological Hamiltonians, which support edge states in Floquet space, and will investigate their topological stabilization.