Author: Johann Kroha
Chiral edge dynamics and quantum Hall physics in synthetic dimensions with an atomic erbium Bose-Einstein condensate (C5)
Roberto Vittorio Roell, Arif Warsi Laskar, Franz Richard Huybrechts, and Martin Weitz
Phys. Rev. A 107, 043302 (2023)
The group led by Martin Weitz succeeded in realizing quantum Hall physics in an effectively two-dimensional Bose-Einstein condensate of neutral erbium atoms, where one dimension is a real, continuous dimension (spatial x direction) and the other is a synthetic dimension created by the discrete, internal angular-momentum degree of freedom (magnetic quantum number) of the erbium ground state. These magnetic angular-momentum substates are Zeeman split in a real magnetic field B perpendicular to the x direction by an equidistant energy Δ [Fig. 1 (a)]. Erbium was chosen because of its large angular momentum J=6, leading to (2J+1)=13 lattice sites in the synthetic dimension. Hopping between the synthetic lattice sites or Zeeman substates is induced as resonant Raman transitions induced as absorption-reemission processes (or vice versa) from two counterpropagating laser beams with relative detuning Δ/h [Fig. 1 (b)]. In this way, each hopping in the synthetic direction is accompanied by a double recoil momentum transfer from the laser photons to the erbium atoms in real space (with c the speed of light). This induces a chiral coupling between the motion in the real and the synthetic dimension. The momentum transfer imprints a position-dependent, chiral phase on the erbium wave function which can be seen as a synthetic vector potential. Incorporating this in the Hamiltonian of free erbium atoms leads to the quantum Hall Hamiltonian in the Landau gauge and, hence, to equally-spaced Landau levels with no dispersion in the bulk of the system. A momentum-dependent dispersion appears only due to finite-size effects near the edges of the system, as seen in Fig. 1 (c).
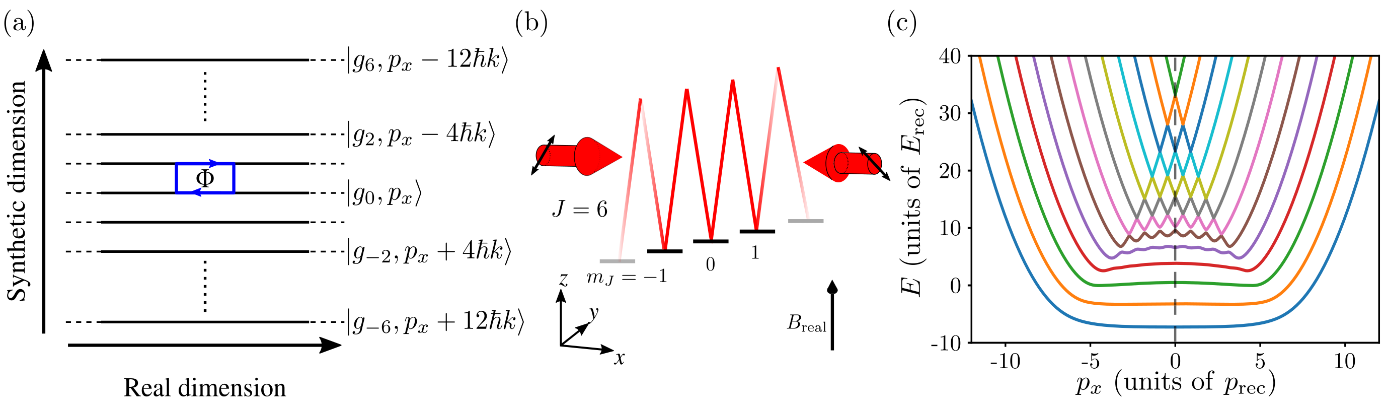
Fig. 1: Schemaitics of creating an artificial quantum Hall system using synthetic dimension and resonant Raman coupling. [R. V. Roell et al., Phys. Rev. A 107, 043302 (2023)]
Using this setup, the researhcers around Martin Weitz could observe time-dependent cyclotron orbits in the bulk as well as skipping orbits at the boundaries of the synthetic two-dimensional system, see Fig. 2.
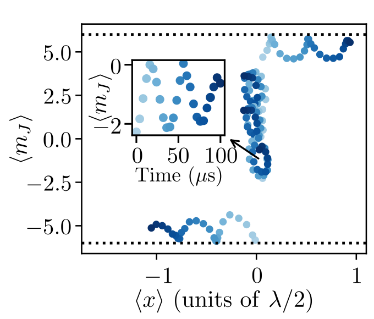
Fig 2.: Temporal evolution of atomic wave packets along the real-space dimension (horizontal axis) and synthetic dimension (vertical axis) following excitation to the next higher band by giving a velocity kick of prec/m for different initial conditions. The color code represents time progressing from bright to dark blue. [R. V. Roell et al., Phys. Rev. A 107, 043302 (2023)]
Fluctuation dissipation relation for a Bose-Einstein condensate of photons (B1)
Fahri Emre Ötztürk, Frank Vewinger, Martin Weitz, and Julian Schmitt
Phys. Rev. Lett. 130, 033602 (2023)
Bose-Einstein condensates of light are unique systems in that the condensation occurs out of a thermal cloud of photons in thermodynamic equilibrium with a reservoir of molecular excitations, which they have in common with black-body radiation, while the phase coherence of the photons in a single mode bears similarities to a laser. This dual nature is exemplified by the equilibrium Bose-Einstein spectral distribution in the condensed phase of the photon gas, while non-Hermitian temporal relaxation dynamics has been observed as well.
In the present work, Fahri Ötztürk, Frank Vewinger, Martin Weitz and Julian Schmitt further characterize this system by analyzing the fluctuation-dissipation relation. The fluctuation-dissipation theorem states that in thermodynamic equilibrium the expectation value of the statistical fluctuations of a system and the (linear) response function with respect to an external perturbation are related by a scaling function which is proportional to the temperature. It is, thus, a unique test case for equilibrium and provides a way of measuring the system temperature. In the present photon gas system coupled to a molecule reservoir by emission and re-absortion processes, the photon number <n> in the optical cavity can be controlled by the cavity detuning Δ, i.e., the difference between the molecule emission frequency and the cavity resonance frequency. Thus, the photon-number fluctuations were measured as thetemporally averaged g2(t) density correlation function, while the response was measured by varying the cavity detuning, d<n>/dΔ. Fig. 3 (a) shows that both functions scale on top of each other over the complete range from strong detuning (small exchange rate of photons with the reservoir, canonical) to small detuning (strong exchange rate, grand-canonical ensemble), with a detuning-independent scale factor temperature, close to ambient temperature, as seen in Fig. 3 (b). Importantly, this clarifies the thermal-equilibrium nature of the open photon Bose-Einstein condensate, as long as the perturbations are within the linear-response regime.
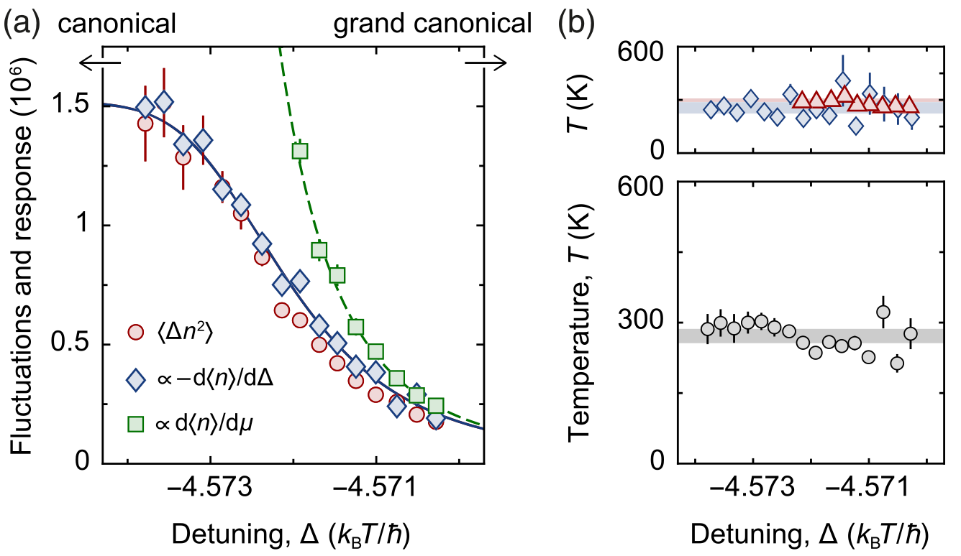
Fig. 3: (a) Fluctuation-dissipation relation of a photon Bose-Einstein condensate depending on the cavity detuning. (b) Within measurement precision, the scaling factor temperature of the fluctuation-dissipation relation is independent of the cavity detuning for various values of the total excitation density X. [F. E. Ötztürk et al., Phys. Rev. Lett. 130, 033602 (2023)]
Controlling superfluid flows using dissipative impurities (B2, B3)
Martin Will, Jamir Marino, Herwig Ott, and M Fleischhauer
SciPost Phys. 14, 064 (2023)
Inducing a superfluid current in a neutral Bose-Einstein condensate is relevant for various applications, but is a difficult task, because a density gradient or a chemical potential (voltage) difference cannot easily be applied.
In the present work, the experimental-theoretical OSCAR team of Martin Will, Jamir Marino, Herwig Ott, and Michael Fleischhauer propose to use noisy impurities to induce superfluid flow in Bose-Einstein condensates. Such an impurity may be experimentally realized by multi-color laser beams which generate a temporally fluctuating optical potential. The dynamics of the condensate in the presence of the impurity is simulated by the Gross-Pitaevskii equation with a weak repulsive nonlinearity and a stochastic term with a Wiener delta-correlated, random potential. The temporal fluctuations deplete the condensate density n(t,x) near the impurity and, thus, effectively act as a sink for the condensate and induce supercurrents towards the impurity, as seen in Fig.4 a), b) for weak and strong fluctuations, respectively. At the same time, the normal density is increased and generates a normal counterflow exactly balancing the superflow [insets of Fig. 4 a), b)]. In this case of a moving condensate of speed v relative to the localized impurity, the spatial density profile naturally becomes asymmetric around the impurity. Fig. 4 c) shows the time- and space averaged supercurrent depending on the noise strength σ. For weak fluctuations the current increases linearly with the noise strength, while for strong fluctuations the system enters a Zeno regime where the strong fast oscillations of n(t,x) average out and the average current decreases with increasing noise. By further increasing the backfround speed v of the condensate, the system enters into an unstable regime where the impurity emits outward-propagating, spatially confined solitons.
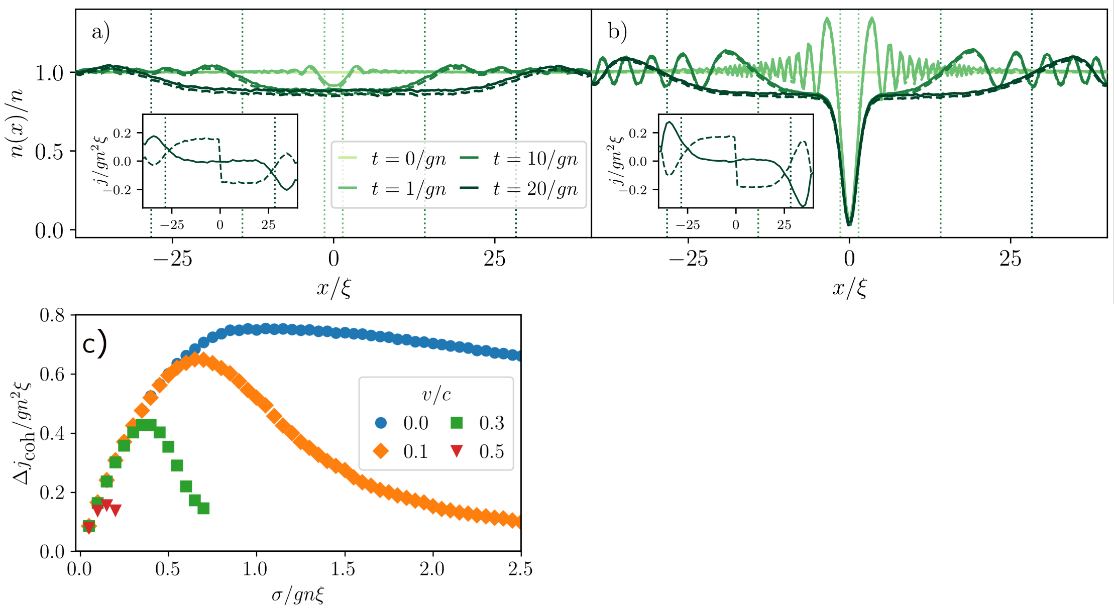
Fig. 4: Position x dependent superconducting density at several snapshots t for a) weak and b) strong fluctuations. The condensate depletion propagates outward with the speed of sound. The insets show the time-averaged supercurrent towards the impurity at x=0 (dashed curves) and the total current (solid lines) compensated by the super and normal flows. c) Noise-induced supercurrent as function of the noise strength for several background speeds v. [M. Will et al., SciPost Phys. 14, 064 (2023)]
