Author: Simon Stellmer
Chiral edge dynamics of cold erbium atoms in the lowest Landau level of a synthetic quantum Hall system
Roberto Vittorio Roell, Arif Warsi Laskar, Franz Richard Huybrechts, and Martin Weitz
Phys. Rev. A 107, 043302 (2023)
Here it is: the first and eagerly awaited paper by the Weitz group on the route to fractional quantum Hall physics. This experiment is based on the somewhat exotic element erbium, which comes with a bundle of unusual properties. One of these properties is the large ground state spin J = 6, giving rise a total of 13 magnetic substates. These states, almost approaching a continuum, are now used to encode a synthetic dimension. Together with one real spatial dimension, this forms a two-dimensional space in which quantum Hall physics can be explored.
The Hall effect sure relies on the charge of a particle, onto which a Lorentz force through an external magnetic field can act. Now, the experiment of Martin Weitz used ultracold ensembles of neutral atoms, which carry no net charge. But there exists a well-established alternative: Raman beams are used to connect neighboring Zeeman states, inducing spin-orbit coupling and leading to a circular path along a trajectory that’s comprised of one spatial dimension and one synthetic “spin” dimension. Now, what would one expect in the classical Hall effect that includes drift along the conductor? For cyclotron orbits smaller than the width of the conductor, charge carriers will follow circular orbits in the bulk of the conductor. On the edges, however, the circular orbits are cut off by the boundary, and the charge carrier “crawls” along the edge: this is called a chiral edge current and beautifully observed in the experiment; see Figure (b) below.
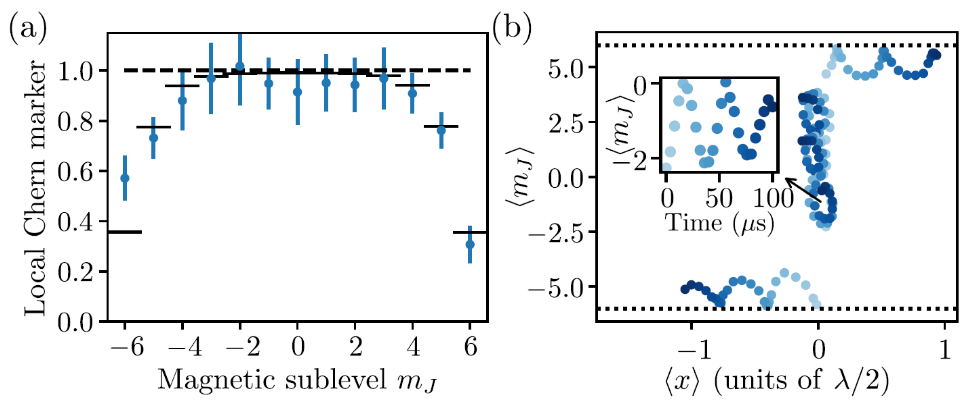
To characterize the system, the authors used a parameter called the local Chern marker. The value of the Chern marker is 1 for an infinite bulk system, and 0 outside the bulk. As shown in Figure (a), the “central” magnetic substates with absolute values smaller than about |mJ| = 3 are sufficiently well in the bulk of magnetic substates to show a Chern marker close to unity. This proves that the multitude of sublevels in erbium allows to reach the Hall regime. This result is the highlight of the PhD work of Roberto Röll, and opens the avenue towards the realms of the fractional quantum Hall physics.
Dynamical phase transition in an open quantum system
Ling-Na Wu, Jens Nettersheim, Julian Feß, Alexander Schnell, Sabrina Burgardt, Silvia Hiebel, Daniel Adam, André Eckardt, and Artur Widera
Another impressive publication by the Kaiserslautern group of Artur Widera, right within the center of OSCAR’s research focus. This work is about phase transitions: phase transitions are ubiquitous in a vast number of physical systems, and the team of authors is pushing well beyond the standard water-and-ice scenario. Specifically, they are investigating a dynamical phase transition of a system that includes individual few Cs atoms that are couples to a bath of Rb atoms, thus forming an open quantum system. Substantial theory input from the TU Berlin group of André Eckardt makes this work a comprehensive study on a very timely field of research.
Typical phase transitions are induced through the change of an external parameter, e.g., temperature or pressure or external fields. Dynamical phase transitions, however, are driven through the time as the control parameter. Such phase transitions have been predicted, experimentally observed and studied in recent years, often in the context of thermalization, in isolated systems. Here, the authors go a step further to study the evolution of the spin composition of an ensemble of atoms in the presence of a bath.
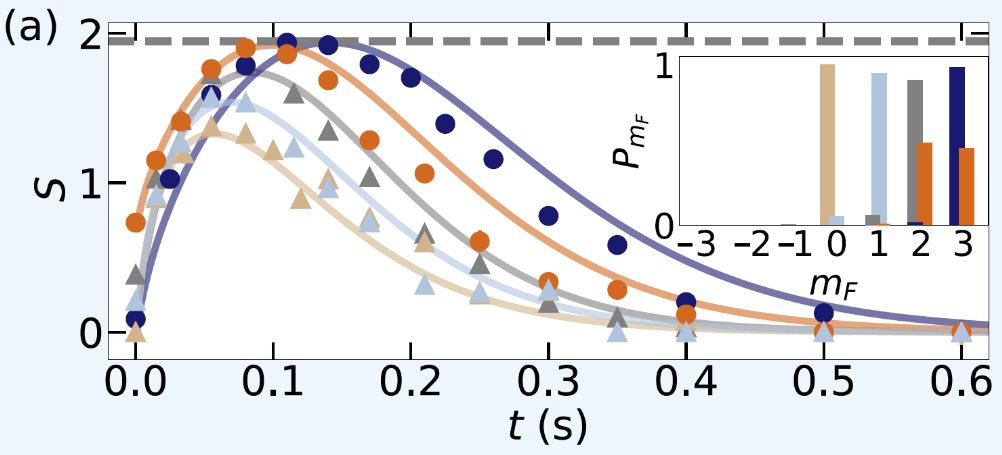
The experimentalists prepare the Cs atoms in a certain excited spin state. Now, depending on the applied magnetic field, spin transitions through exchange with the Rb bath can happen only towards lower mF quantum number (exoergic, at high fields) or in both directions (endoergic, at low fields). The spin entropy, measure of the spin composition, is measured over time. An example for high magnetic fields, allowing only for relaxation from large “up” to small “down” spin states, is shown in the Figure below. For all initial state preparations, the entropy first increases and then settles to an equilibrium value. Strikingly, for many initializations, the spin entropy reaches the maximum possible value. As described in the publication, this behavior is a signature of a continuous phase transition under the control of time.
Symmetry-protected transport through a lattice with a local particle loss
A.-M. Visuri, T. Giamarchi, and C. Kollath
Phys. Rev. Lett. 129, 056802 (2022)
Is dissipation really as bad as we thought? Can we even turn dissipation into a useful tool to stabilize quantum states? These questions are at the very heart of the CRC OSCAR, and fresh theory paper along these lines just emerged from the printing press. Let’s consider transport through a chain of atoms or ions. Naively, one would expect that particle loss in the chain would destroy the conductance of the system entirely. Luckily, in a quantum system, this is not necessarily the case.
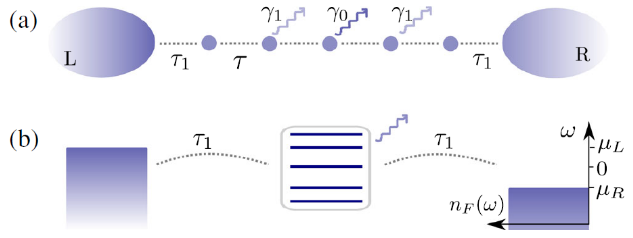
The experimental scenario considered by the group of Corinna Kollath is depicted above. Two reservoirs of different chemical potential are connected via a chain of M sites. The strongest particle loss occurs on a central site. Now, for an isolated lattice, half of the eigenstates are antisymmetric and have a node at the site of the particle loss. Particles in these antisymmetric eigenstates “survive”, and transport through these eigenstates is not affected. Therefore, removing a particle at a specific site, very different to removing a piece from classical copper wire, does not fully destroy the transport properties of the entire system. This finding is somewhat surprising and shows the power of symmetries in these systems.
Lead author Anne-Maria Visuri from Bonn performed this work with a certain experiment in mind: the cold-atom experiment in the group of Herwig Ott in Kaiserslautern, which has an electron beam built-in to precisely remove individual atoms from a lattice. The finite size of the electron beam might also affect adjacent lattice sites: that’s why a smaller loss probability is introduced for adjacent sites as well. Reassuringly for the experimentalists, transport through the lattice persists even if neighboring sites are mildly disturbed.
This work opens up a range of new possible directions: What if the lattice was formed by bosonic atoms or atoms with strong interactions? What if the lattice was replaced by a correlated insulator or a superfluid? On what timescales does the steady-state form after the event of a particle loss? As many platforms are available to study these questions, we are looking forward to experimental realizations.
